Optimization problem

Both control system and planner are based on a Model Predictive Contouring Control (MPCC), a particular kind of predictive control used to follow a reference curve parametrized by arc length θ ∈ [0, L], with L the total circuit length.

All MPCCs find the input signals to apply to the system by solving an optimization problem: in this case the objective function is about maximizing the space travelled and minimizing the distance errors between the real car and a virtual point moving along the center line of the track, whose velocity is a variable of the problem. The constraints deal with state variables admissible range, circuit border and car nonlinear dynamics.

In order to use this controller in a (soft) real-time environment, it is necessary to transform this highly nonlinear problem into a simpler one consisting of a quadratic objective function and linear constraints, so that it can be solved by a quadratic solver.

Control system

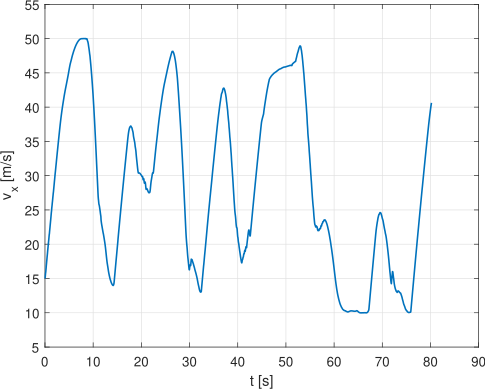
The control algorithm works exactly as a normal MPC: at each sampling time it solves the quadratic problem on a fixed time horizon and uses only the first computed input to drive the car, discarding the other ones and repeating the process at the following time.

Trajectory planner

The trajectory planner is completely based on the control system. The main difference is that the latter has equations which are function of time, hence the prediction performed by the model is a fixed time in the future. On the other hand, planner equations are function of the coordinate θ, predicting the behaviour of the system in the following meters.

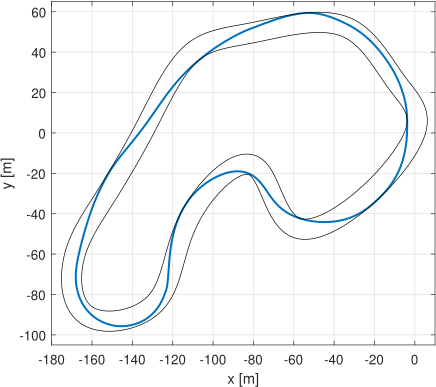
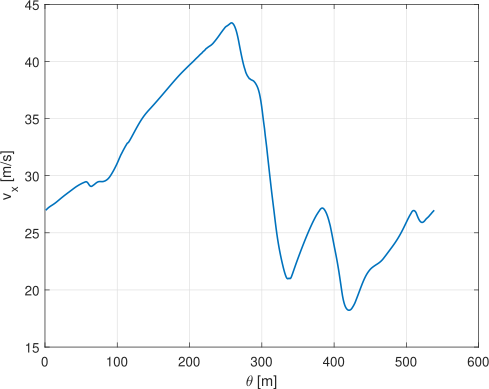
It is therefore possible to set a prediction distance equal to the circuit length, in order to compute the best trajectory on a whole lap. The last modification consists of imposing the equality between initial and final state as a new constraint of the problem, so that it is independent of the starting conditions of the car.

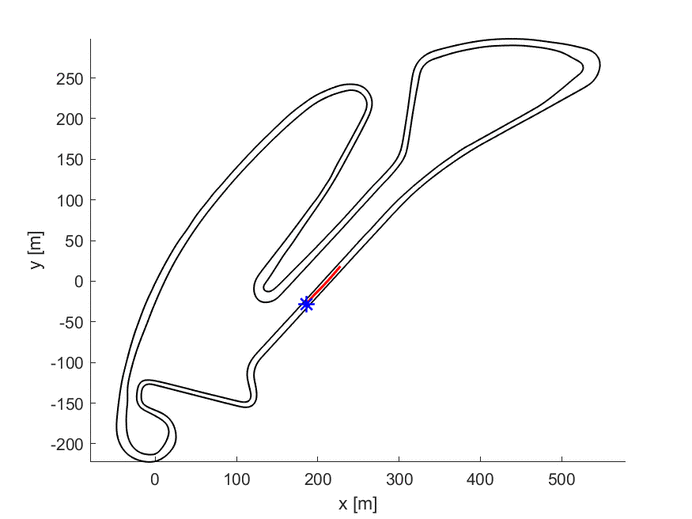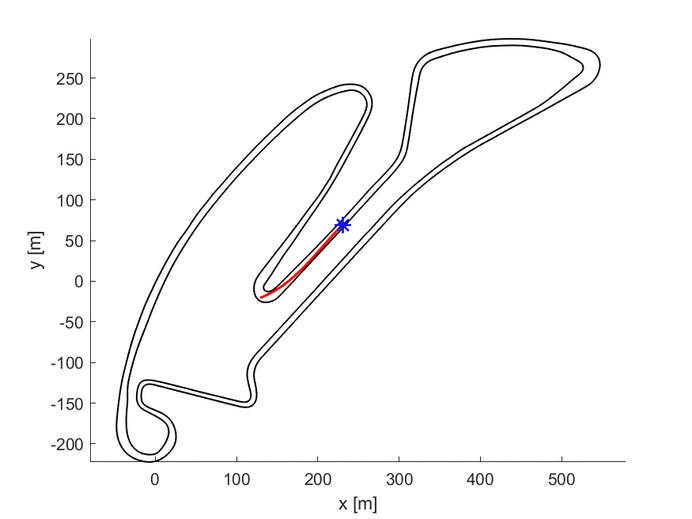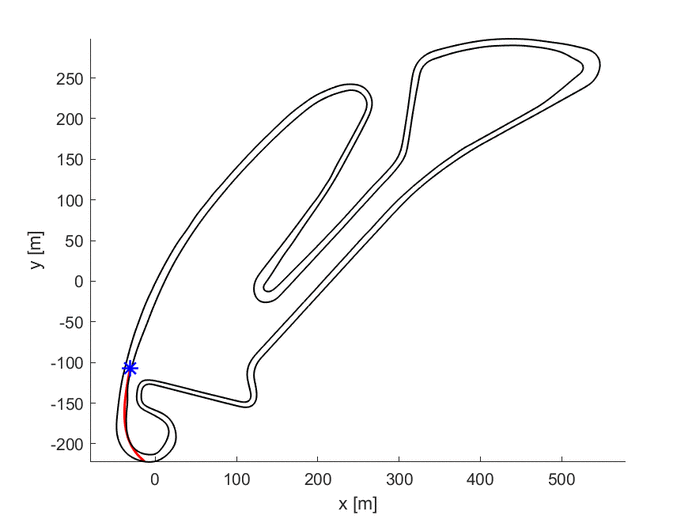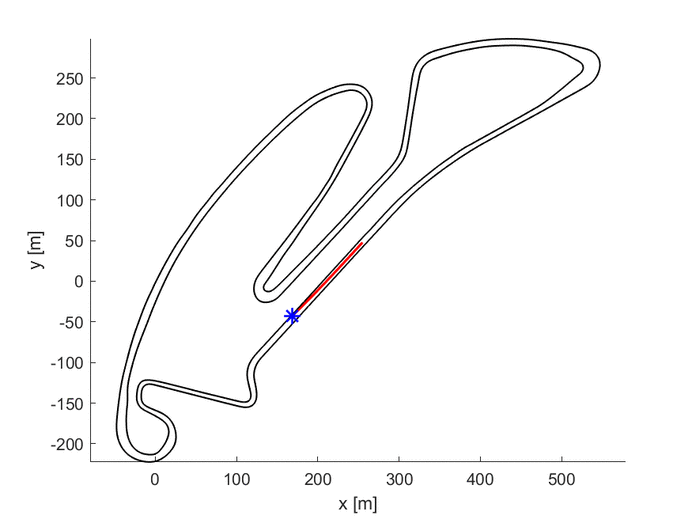
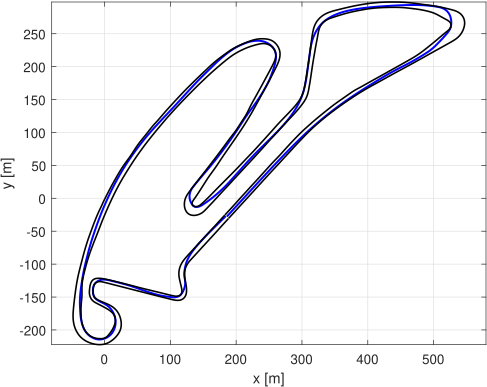
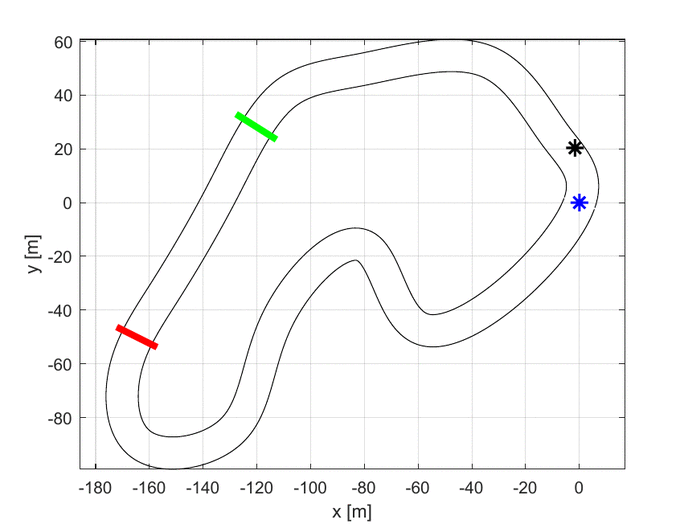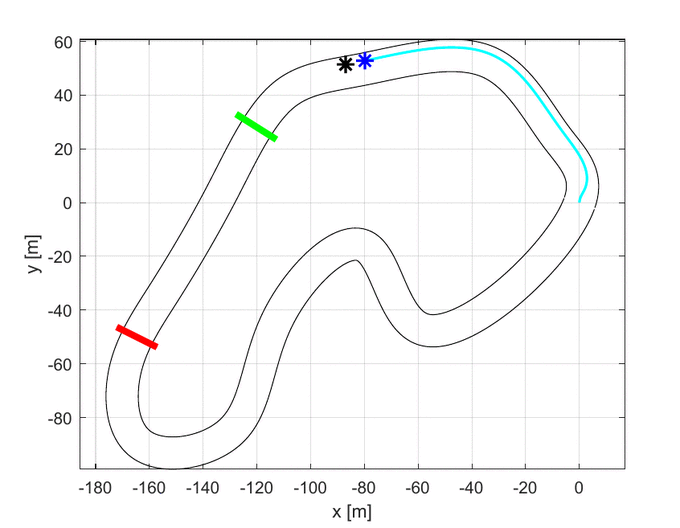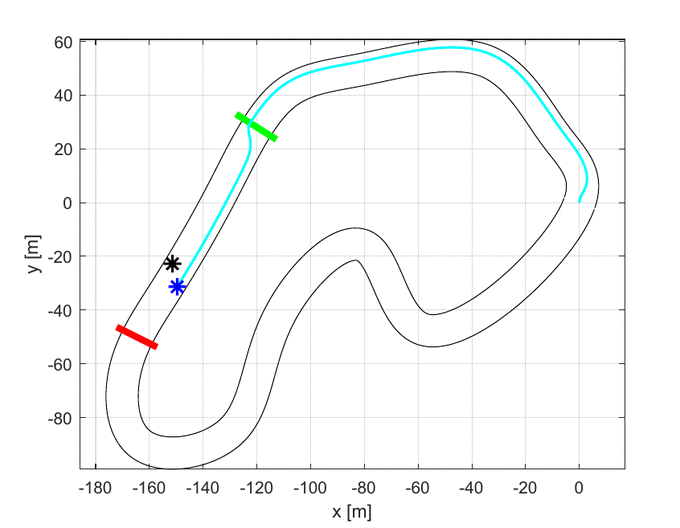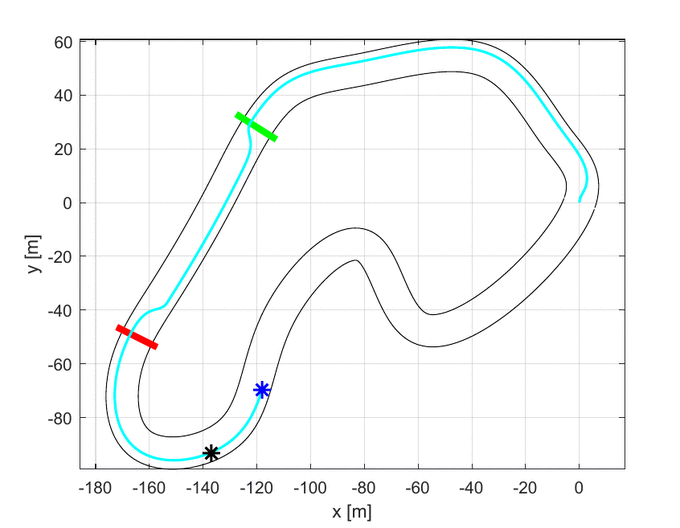
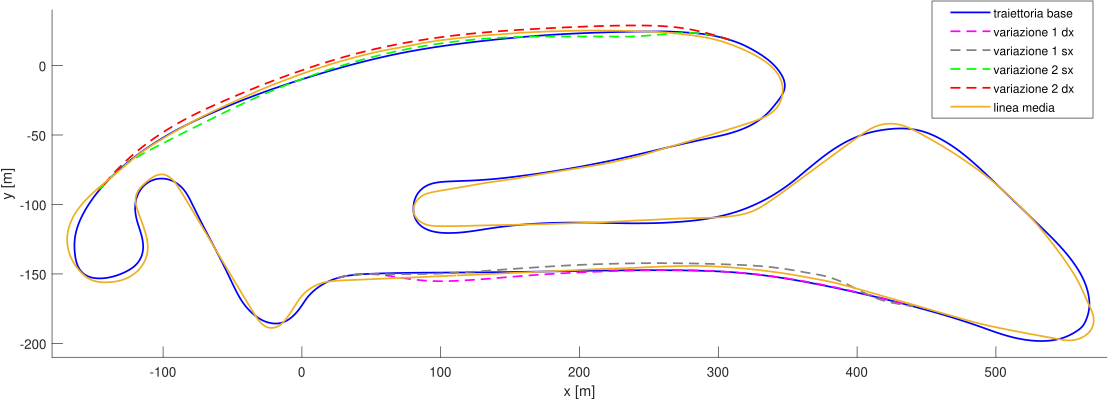
As it is possible to see in the upper GIF, the algorithm starts with the center line as the first guess and, step by step, it improves the trajectory until it finds the one with the lowest travel time.

Overtakes

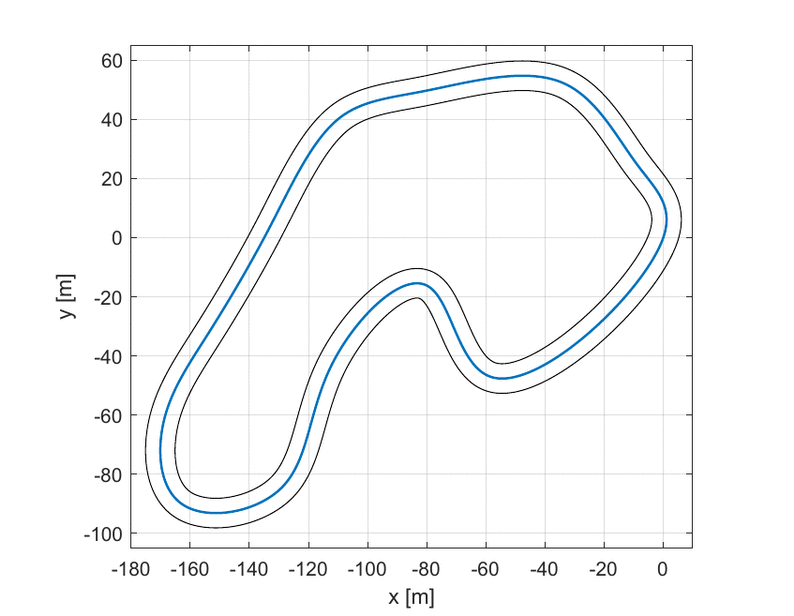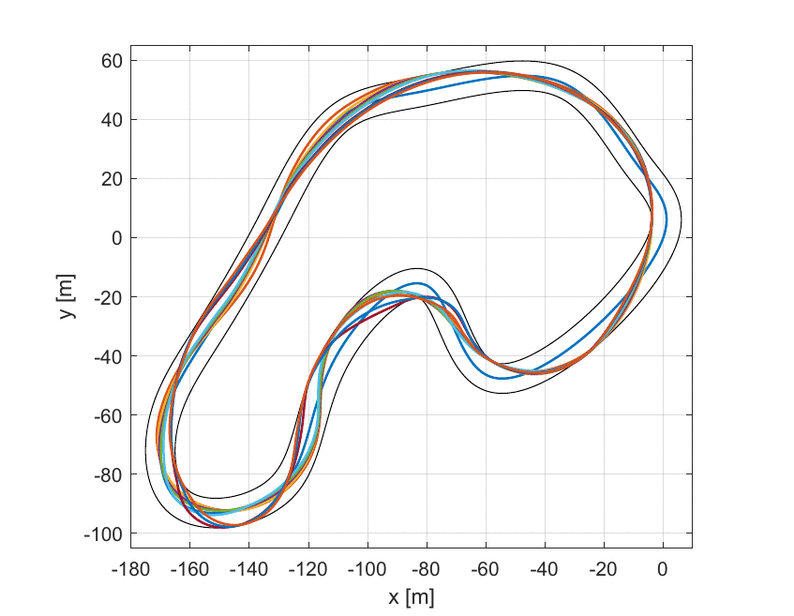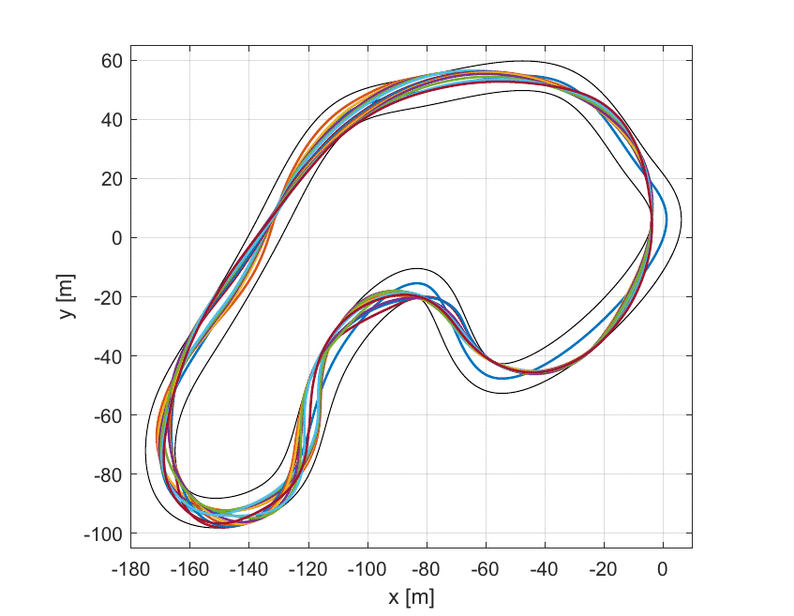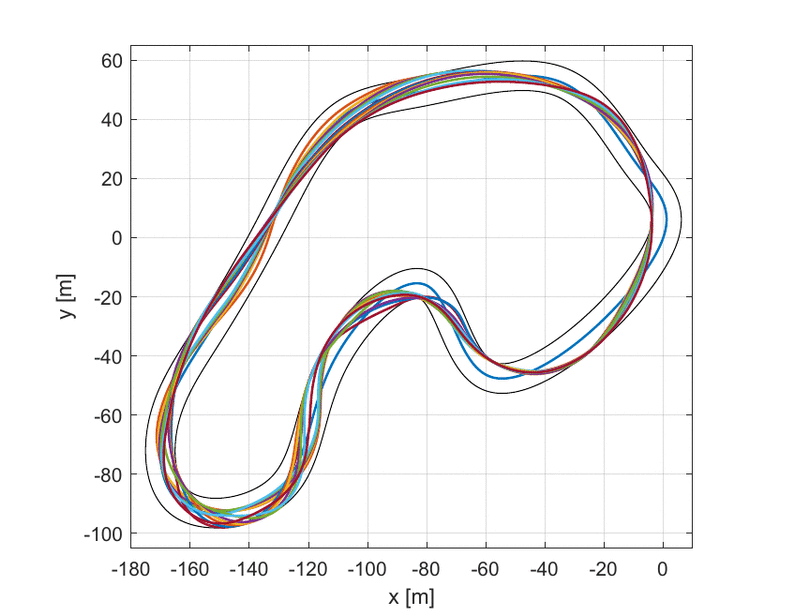
Overtakes are just permitted in predefined track sectors and only if the opposing car is in a certain range. The cars involved in the overtake must run across the sides of the track without interfering each other.

The trajectory planner was also used to compute the variations from the main trajectory in order to perform these actions, with the constraint to return on it at the end of the overtake.